Twierdzenie Pitagorasa

Oto postać, która co roku sprawia trudności sporej liczbie uczniów gimnazjów, ale także nauczycieli.

Rzeczywiście, ten człowiek dawno temu pozostawił nam twierdzenie i każdego roku wielu uczniów próbuje zrozumieć i zapamiętać jego równanie.

Z roku na rok Twoi nauczyciele muszą pomagać Ci odkrywać, rozumieć i uczyć się tego twierdzenia.

Chcę tu porozmawiać o Pitagoras.

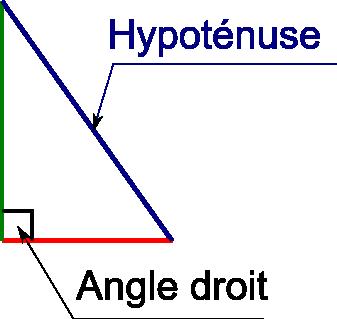
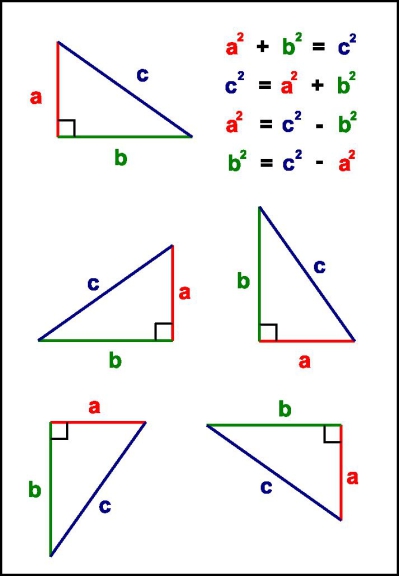
TO Twierdzenie Pitagorego można wyrazić następująco: „ W trójkącie prostokątnym kwadrat przeciwprostokątnej jest równy sumie kwadratów dwóch pozostałych boków.”

L’ Przeciwprostokątna reprezentuje w trójkąt prostokątny, TO Przeciwna strona naprosty kąt.

Można zauważyć, że niezależnie od kierunku naszego trójkąta równanie się nie zmienia, ale z drugiej strony można je zapisać na różne sposoby.

Pozostaje ustalić, jak znaleźć liczbę, która pomnożona przez siebie daje wynik znaleziony w równaniu. (Pierwiastek kwadratowy)

a x a = a²

b x b = b²

c x do = c²

Jeśli jeszcze nie opisałeś, jak obliczyć a pierwiastek kwadratowy, weź kalkulator i naciśnij klawisz pierwiastek kwadratowy reprezentowany przez ten znak √

Przykład zrozumienia tego twierdzenia.

a = 3

b = 4

c =?

Wiemy zatem, że: a² + b² = c²

a² = 3² = 3 x 3 = 9

b² = 4² = 4 x 4 = 16

a² + b² = c²
9 + 16 = 25

c² = 25

do x do = 25

c = 5